Depois de cobrir a teoria, criaremos um projeto JavaScript. Isso nos ajudará a visualizar mais facilmente a fórmula em ação usando Chart.js para representar os dados.
O que é esse método e por que usá-lo?
Mínimos quadrados é um método para aplicar regressão linear. Isso nos ajuda a prever resultados com base em um conjunto existente de dados, bem como anomalias claras em nossos dados. Anomalias são valores muito bons ou ruins para serem verdadeiros ou que representam casos raros.
Por exemplo, digamos que temos uma lista de quantos tópicos os futuros engenheiros aqui no freeCodeCamp podem resolver se investirem 1, 2 ou 3 horas continuamente. Então, podemos prever quantos tópicos serão cobertos após 4 horas de estudo contínuo, mesmo sem esses dados estarem disponíveis para nós.
Este método é usado por vários profissionais, por exemplo, estatísticos, contadores, gerentes e engenheiros (como em problemas de aprendizado de máquina).
Configurando um exemplo
Antes de pularmos para a fórmula e o código, vamos definir os dados que usaremos.
Para fazer isso, vamos expandir o exemplo mencionado anteriormente.
Vamos supor que nosso objetivo seja descobrir quantos tópicos são abordados por um aluno por hora de aprendizado.
Cada par (X, Y) representará um aluno. Como todos temos diferentes taxas de aprendizado, o número de tópicos resolvidos pode ser maior ou menor pelo mesmo tempo investido.
| Horas (X) | Tópicos resolvidos (Y) |
|---|---|
| 1 | 1,5 |
| 1,2 | 2 |
| 1,5 | 3 |
| 2 | 1.8 |
| 2,3 | 2,7 |
| 2,5 | 4,7 |
| 2,7 | 7,1 |
| 3 | 10 |
| 3,1 | 6 |
| 3,2 | 5 |
| 3,6 | 8,9 |
Você pode ler assim: “Alguém passou 1 hora e resolveu 2 tópicos” ou “Um aluno após 3 horas resolveu 10 tópicos”.
Em um gráfico, esses pontos se parecem com isto:
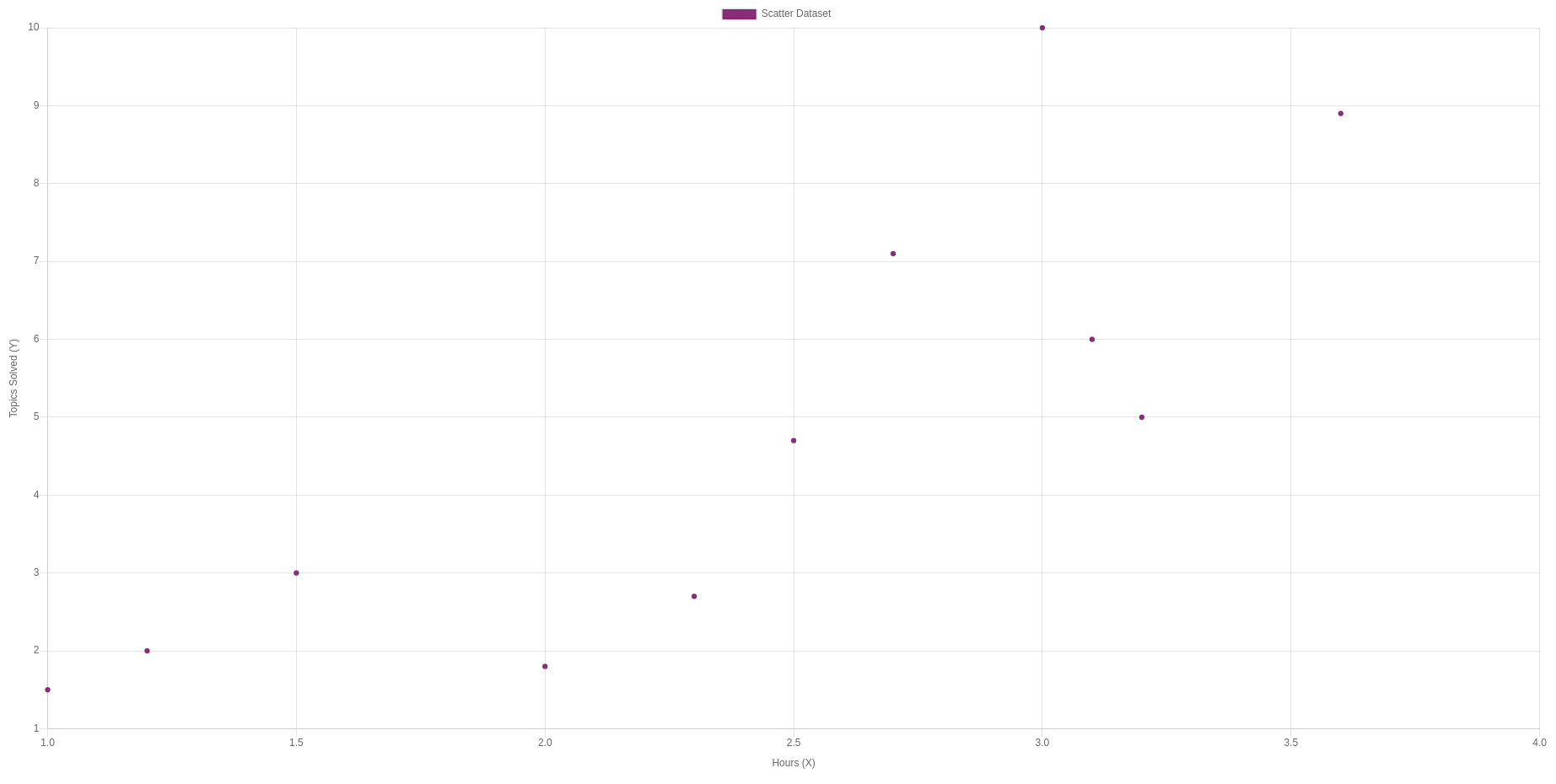
Aviso Legal: Esses dados são fictícios e foram obtidos por meio de teclas aleatórias. Não tenho ideia dos valores reais.
A fórmula
Y = a + bX
A fórmula, para quem não está familiarizado com ela, provavelmente parece nada assombrosa – ainda mais dado o fato de que já temos os valores para Y e X em nosso exemplo.
Dito isso, e agora que não temos medo da fórmula, só precisamos descobrir o uma e b valores.
Para dar algum contexto sobre o que eles significam:
- uma é a interceptação, ou seja, o valor que esperamos, em média, de um aluno que pratica por uma hora. Uma hora é a menor quantidade de tempo que aceitaremos em nosso conjunto de dados de exemplo.
- b é a inclinação ou coeficiente, ou seja, o número de tópicos resolvidos em uma hora específica (X). Conforme aumentamos em horas (X) passou estudando, b aumenta mais e mais.
Calculando “b”
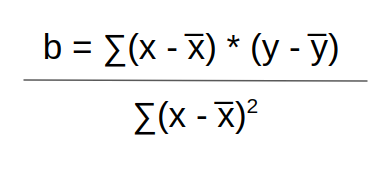
X e Y são as nossas posições da nossa tabela anterior. Quando eles têm um – (mácron) acima deles, significa que devemos usar a média que obtemos somando todos eles e dividindo pelo valor total:
͞X -> 1 + 1,2 + 1,5 + 2 + 2,3 + 2,5 + 2,7 + 3 + 3,1 + 3,2 + 3,6 = 2,37
͞Y -> 1,5 + 2 + 3 + 1,8 + 2,7 + 4,7 + 7,1 + 10 + 6 + 5 + 8,9 / 11 = 4,79
Agora que temos a média, podemos expandir nossa tabela para incluir os novos resultados:
| Horas (X) | Tópicos resolvidos (Y) | (X – ͞x) | (y – ͞y) | (X – ͞x) * (y – ͞y) | (x – ͞x) ² |
|---|---|---|---|---|---|
| 1 | 1,5 | -1,37 | -3,29 | 4,51 | 1,88 |
| 1,2 | 2 | -1,17 | -2,79 | 3,26 | 1,37 |
| 1,5 | 3 | -0,87 | -1,79 | 1,56 | 0,76 |
| 2 | 1.8 | -0,37 | -2,99 | 1,11 | 0,14 |
| 2,3 | 2,7 | -0,07 | -2,09 | 0,15 | 0,00 |
| 2,5 | 4,7 | 0,13 | -0,09 | -0,01 | 0,02 |
| 2,7 | 7,1 | 0,33 | 2,31 | 0,76 | 0,11 |
| 3 | 10 | 0,63 | 5,21 | 3,28 | 0,40 |
| 3,1 | 6 | 0,73 | 1,21 | 0,88 | 0,53 |
| 3,2 | 5 | 0,83 | 0,21 | 0,17 | 0,69 |
| 3,6 | 8,9 | 1,23 | 4,11 | 5.06 | 1,51 |
O estranho símbolo sigma (∑) nos diz para resumir tudo:
∑ (x – ͞x) * (y – ͞y) -> 4,51 + 3,26 + 1,56 + 1,11 + 0,15 + -0,01 + 0,76 + 3,28 + 0,88 + 0,17 + 5,06 = 20,73
∑ (x – ͞x) ² -> 1,88 + 1,37 + 0,76 + 0,14 + 0,00 + 0,02 + 0,11 + 0,40 + 0,53 + 0,69 + 1,51 = 7,41
E finalmente fazemos 20,73 / 7,41 e nós temos b = 2,8
Nota: Ao usar uma calculadora de entrada de expressão, como a que está disponível no Ubuntu, -2² retorna -4 em vez de 4. Para evitar essa entrada (-2) ².
Calculando “a”
Tudo o que resta é uma, para o qual a fórmula é ͞͞͞Y = a + b ͞x. Já obtivemos todos esses outros valores, então podemos substituí-los e obter:
- 4,79 = uma + 2,8 * 2,37
- 4,79 = uma + 6,64
- uma = -6,64 + 4,79
- a = -1,85
O resultado
Nossa fórmula final se torna:
Y = -1,85 + 2,8 * X
Agora vamos substituir o X em nossa fórmula com cada valor que temos:
| Horas (X) | -1,85 + 2,8 * X |
|---|---|
| 1 | 0,95 |
| 1,2 | 1,51 |
| 1,5 | 2,35 |
| 2 | 3,75 |
| 2,3 | 4,59 |
| 2,5 | 5,15 |
| 2,7 | 5,71 |
| 3 | 6,55 |
| 3,1 | 6,83 |
| 3,2 | 7,11 |
| 3,6 | 8,23 |
Que é um gráfico semelhante a este:
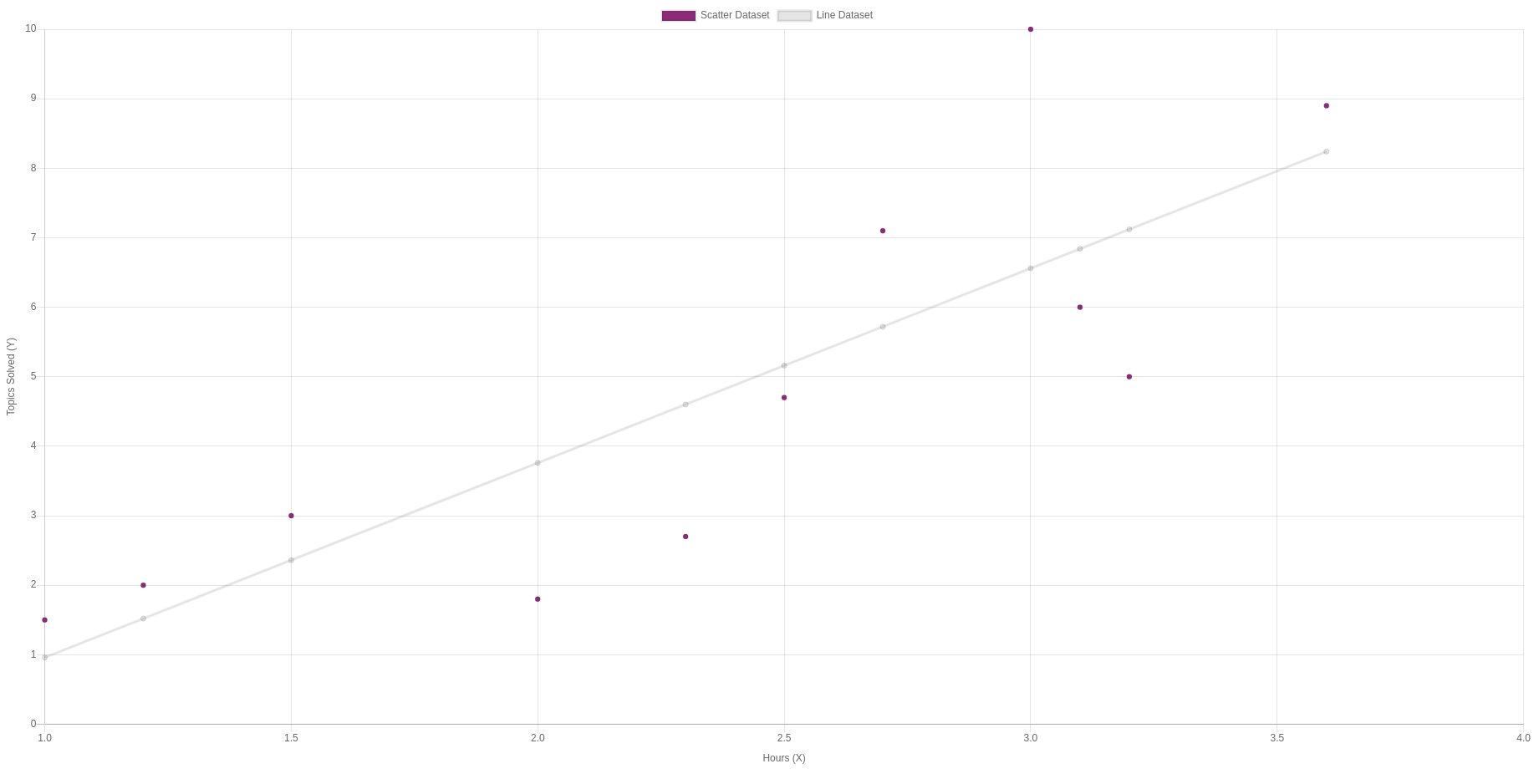
Se quisermos prever quantos tópicos esperamos que um aluno resolva com 8 horas de estudo, nós o substituímos em nossa fórmula:
- Y = -1,85 + 2,8 * 8
- Y = 20,55
Em um gráfico, podemos ver:
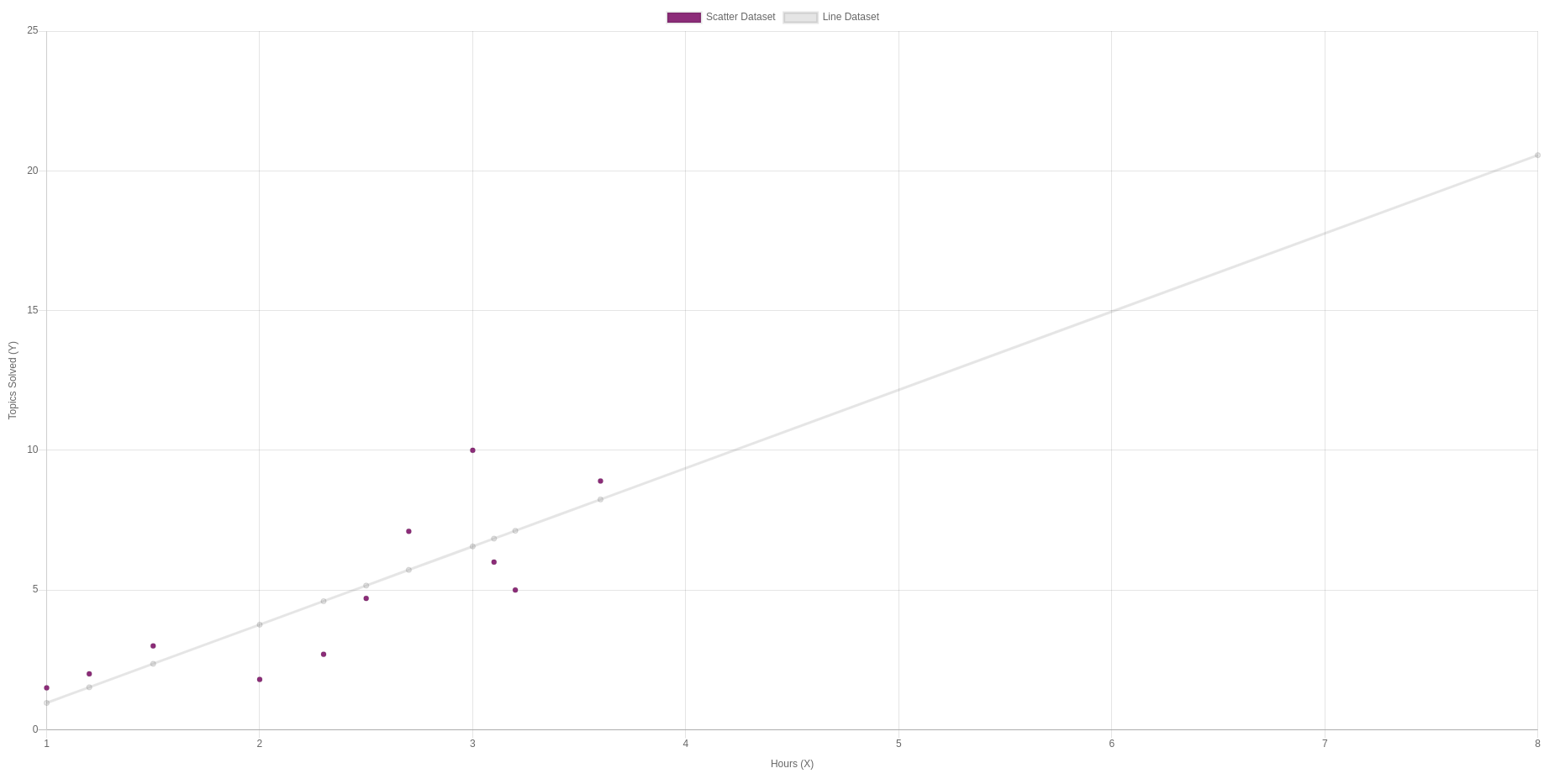
Limitações
Sempre tenha em mente as limitações de um método. Esperamos que isso o ajude a evitar resultados incorretos.
E esse método, como qualquer outro, tem suas limitações. Aqui estão algumas:
- Não leva em consideração a complexidade dos temas resolvidos. Um tópico coberto no início do “Certificação de Web Design Responsivo“provavelmente levará menos tempo para aprender e resolver do que fazer um dos projetos finais. Portanto, se os dados que temos forem de diferentes pontos de partida de um curso, as previsões não serão precisas
- É impossível alguém estudar 240 horas continuamente ou resolver mais tópicos do que os disponíveis. Independentemente disso, o método nos permite prever esses valores. Nesse ponto, o método não está mais dando resultados com precisão, pois é uma impossibilidade.
Projeto de amostra
Fazer isso manualmente não é necessário. Podemos criar nosso projeto onde inserimos os valores X e Y, ele desenha um gráfico com esses pontos e aplica a fórmula de regressão linear.
A pasta do projeto terá o seguinte conteúdo:
src/ |-public // folder with the content that we will feed to the browser |-index.html |-style.css |-least-squares.js package.json server.js // our Node.js serverE package.json:
{ "name": "least-squares-regression", "version": "1.0.0", "description": "Visualize linear least squares", "main": "server.js", "scripts": { "start": "node server.js", "server-debug": "nodemon --inspect server.js" }, "author": "daspinola", "license": "MIT", "devDependencies": { "nodemon": "2.0.4" }, "dependencies": { "express": "4.17.1" }}Assim que tivermos o package.json e executarmos npm install teremos Express e nodemon disponíveis. Você pode trocá-los por outros como preferir, mas eu os uso por conveniência.
No server.js:
const express = require('express')const path = require('path')const app = express()app.use(express.static(path.join(__dirname, 'public')))app.get('/', function(req, res) { res.sendFile(path.join(__dirname, 'public/index.html'))})app.listen(5000, function () { console.log(`Listening on port ${5000}!`)})Este pequeno servidor é feito para que possamos acessar nossa página quando escrevermos no navegador localhost: 5000. Antes de executá-lo, vamos criar os arquivos restantes:
public / index.html
<html> <head> <title>Least Squares Regression</title> <script src="https://cdn.jsdelivr.net/npm/[email protected]/dist/Chart.min.js"></script> <link rel="stylesheet" href="style.css"> </head> <body> <div class="container"> <div class="left-half"> <div> <input type="number" class="input-x" placeholder="X"> <input type="number" class="input-y" placeholder="Y"> <button class="btn-update-graph">Add</button> </div> <div> <span class="span-formula"></span> </div> <div> <table class="table-pairs"> <thead> <th> X </th> <th> Y </th> </thead> <tbody></tbody> </table> </div> </div> <div class="right-half"> <canvas id="myChart"></canvas> </div> </div> <script src="/js/least-squares.js"></script> </body></html>Nós criamos nossos elementos:
- Duas entradas para nossos pares, uma para X e uma para Y
- Um botão para adicionar esses valores a uma tabela
- Um intervalo para mostrar a fórmula atual conforme os valores são adicionados
- Uma tabela para mostrar os pares que adicionamos
- E uma tela para nosso gráfico
Também importamos o Chart.js biblioteca com um CDN e adicione nossos arquivos CSS e JavaScript.
public / style.css
.container { display: grid; }.left-half { grid-column: 1;}.right-half { grid-column: 2;}Adicionamos algumas regras para termos nossas entradas e tabela à esquerda e nosso gráfico à direita. Isso aproveita a grade CSS.
public / least-squares.js
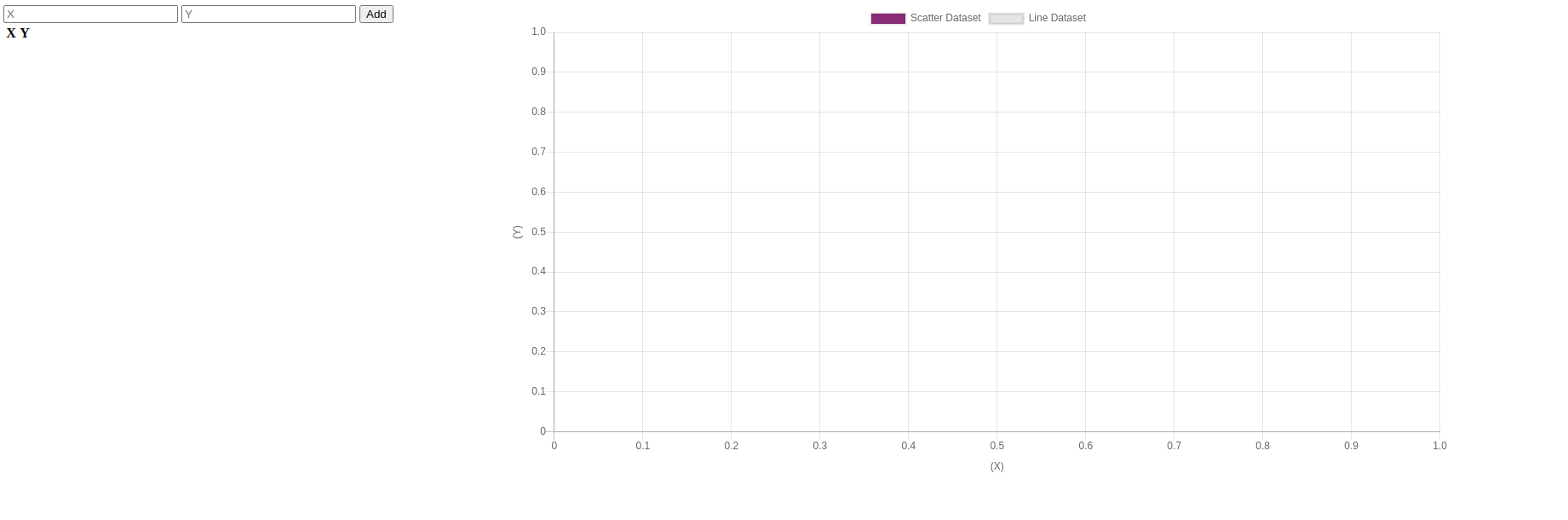
document.addEventListener('DOMContentLoaded', init, false);function init() { const currentData = { pairs: [], slope: 0, coeficient: 0, line: [], }; const chart = initChart();} function initChart() { const ctx = document.getElementById('myChart').getContext('2d'); return new Chart(ctx, { type: 'scatter', data: { datasets: [{ label: 'Scatter Dataset', backgroundColor: 'rgb(125,67,120)', data: [], }, { label: 'Line Dataset', fill: false, data: [], type: 'line', }], }, options: { scales: { xAxes: [{ type: 'linear', position: 'bottom', display: true, scaleLabel: { display: true, labelString: '(X)', }, }], yAxes: [{ type: 'linear', position: 'bottom', display: true, scaleLabel: { display: true, labelString: '(Y)', }, }], }, }, });}E, finalmente, inicializamos nosso gráfico. No início, deve estar vazio, pois ainda não adicionamos nenhum dado a ele.
Agora se corrermos npm run server-debug e abra nosso navegador em localhost: 5000, devemos ver algo assim:
Adicionando funcionalidade
A próxima etapa é fazer com que o botão “Adicionar” faça algo. No nosso caso, queremos alcançar:
- Adicione os valores X e Y à tabela
- Atualize a fórmula quando adicionarmos mais de um par (precisamos de pelo menos 2 pares para criar uma linha)
- Atualize o gráfico com os pontos e a linha
- Limpe as entradas, para que seja mais fácil continuar introduzindo dados
Adicione os valores à tabela
public / least-squares.js
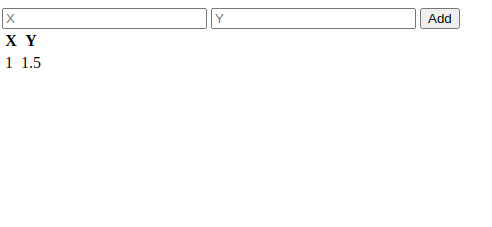
document.addEventListener('DOMContentLoaded', init, false);function init() { const currentData = { pairs: [], slope: 0, coeficient: 0, line: [], }; const btnUpdateGraph = document.querySelector('.btn-update-graph'); const tablePairs = document.querySelector('.table-pairs'); const spanFormula = document.querySelector('.span-formula'); const inputX = document.querySelector('.input-x'); const inputY = document.querySelector('.input-y'); const chart = initChart(); btnUpdateGraph.addEventListener('click', () => { const x = parseFloat(inputX.value); const y = parseFloat(inputY.value); updateTable(x, y); }); function updateTable(x, y) { const tr = document.createElement('tr'); const tdX = document.createElement('td'); const tdY = document.createElement('td'); tdX.innerHTML = x; tdY.innerHTML = y; tr.appendChild(tdX); tr.appendChild(tdY); tablePairs.querySelector('tbody').appendChild(tr); }}// ... rest of the code as it wasPegamos todos os elementos que usaremos em breve e adicionamos um evento no botão “Adicionar”. Esse evento pegará os valores atuais e atualizará nossa tabela visualmente.
Precisamos analisar a quantidade, pois obtemos uma string. Será importante para a próxima etapa, quando tivermos de aplicar a fórmula.
Faça os cálculos
Toda a matemática sobre a qual falamos anteriormente (obtendo a média de X e Y, calculando b, e calculando uma) agora deve ser transformado em código. Também exibiremos o uma e b valores, então os vemos mudando à medida que adicionamos valores.
public / least-squares.js
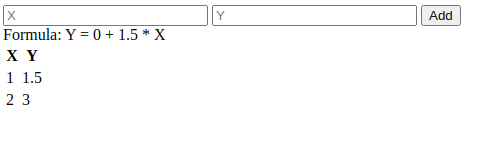
// ... rest of the code as it wasbtnUpdateGraph.addEventListener('click', () => { const x = parseFloat(inputX.value); const y = parseFloat(inputY.value); updateTable(x, y); updateFormula(x, y);});function updateFormula(x, y) { currentData.pairs.push({ x, y }); const pairsAmount = currentData.pairs.length; const sum = currentData.pairs.reduce((acc, pair) => ({ x: acc.x + pair.x, y: acc.y + pair.y, }), { x: 0, y: 0 }); const average = { x: sum.x / pairsAmount, y: sum.y / pairsAmount, }; const slopeDividend = currentData.pairs .reduce((acc, pair) => parseFloat(acc + ((pair.x - average.x) * (pair.y - average.y))), 0); const slopeDivisor = currentData.pairs .reduce((acc, pair) => parseFloat(acc + (pair.x - average.x) ** 2), 0); const slope = slopeDivisor !== 0 ? parseFloat((slopeDividend / slopeDivisor).toFixed(2)) : 0; const coeficient = parseFloat( (-(slope * average.x) + average.y).toFixed(2), ); currentData.line = currentData.pairs .map((pair) => ({ x: pair.x, y: parseFloat((coeficient + (slope * pair.x)).toFixed(2)), })); spanFormula.innerHTML = `Formula: Y = ${coeficient} + ${slope} * X`;}// ... rest of the code as it wasNão há muito a ser dito sobre o código aqui, pois é toda a teoria que vimos anteriormente. Percorremos os valores para obter somas, médias e todos os outros valores de que precisamos para obter o coeficiente (uma) e a inclinação (b)
Nós temos o pares e linha no atual variável, então nós os usaremos na próxima etapa para atualizar nosso gráfico.
Atualize o gráfico e limpe as entradas
public / least-squares.js
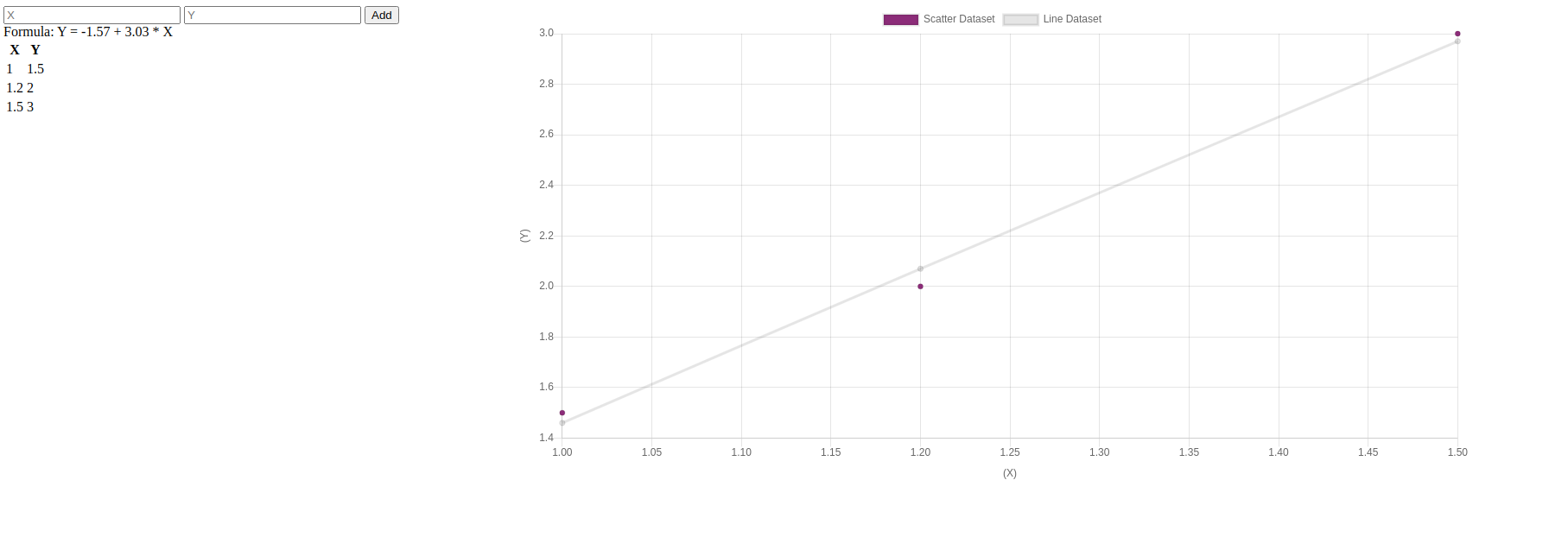
// ... rest of the code as it wasbtnUpdateGraph.addEventListener('click', () => { const x = parseFloat(inputX.value); const y = parseFloat(inputY.value); updateTable(x, y); updateFormula(x, y); updateChart(); clearInputs();});function updateChart() { chart.data.datasets[0].data = currentData.pairs; chart.data.datasets[1].data = currentData.line; chart.update();} function clearInputs() { inputX.value=""; inputY.value="";}// ... rest of the code as it wasAtualizando o gráfico e limpando as entradas de X e Y é muito simples. Temos dois conjuntos de dados, o primeiro (posição zero) é para nossos pares, então mostramos o ponto no gráfico. O segundo (posição um) é para nossa linha de regressão.
Temos que pegar nossa instância do gráfico e chamar atualizar então vemos os novos valores sendo levados em consideração.
Adicionando algum estilo
Podemos mudar nosso layout um pouco para que seja mais gerenciável. Nada importante, apenas serve como um lembrete de que podemos atualizar a IU a qualquer momento
public / style.css
.container { display: grid; }.left-half { grid-column: 1;}.right-half { grid-column: 2;}.pairs-style input[type="number"],.pairs-style button { margin: 5px 0px;}.table-pairs { border-collapse: collapse; width: 100%;}.table-pairs td { text-align: center;}.table-pairs,.table-pairs th,.table-pairs td { margin: 10px 0px; border: 1px solid black;}public / index.html
<html> <head> <title>Least Squares Regression</title> <script src="https://cdn.jsdelivr.net/npm/[email protected]/dist/Chart.min.js"></script> <link rel="stylesheet" href="style.css"> </head> <body> <div class="container"> <div class="left-half"> <div class="pairs-style"> <div> <input type="number" class="input-x" placeholder="X"> </div> <div> <input type="number" class="input-y" placeholder="Y"> </div> <button class="btn-update-graph">Add</button> </div> <div> <span class="span-formula">Formula: Y = a + b * X</span> </div> <div> <table class="table-pairs"> <thead> <th> X </th> <th> Y </th> </thead> <tbody></tbody> </table> </div> </div> <div class="right-half"> <canvas id="myChart"></canvas> </div> </div> <script src="/js/least-squares.js"></script> </body></html>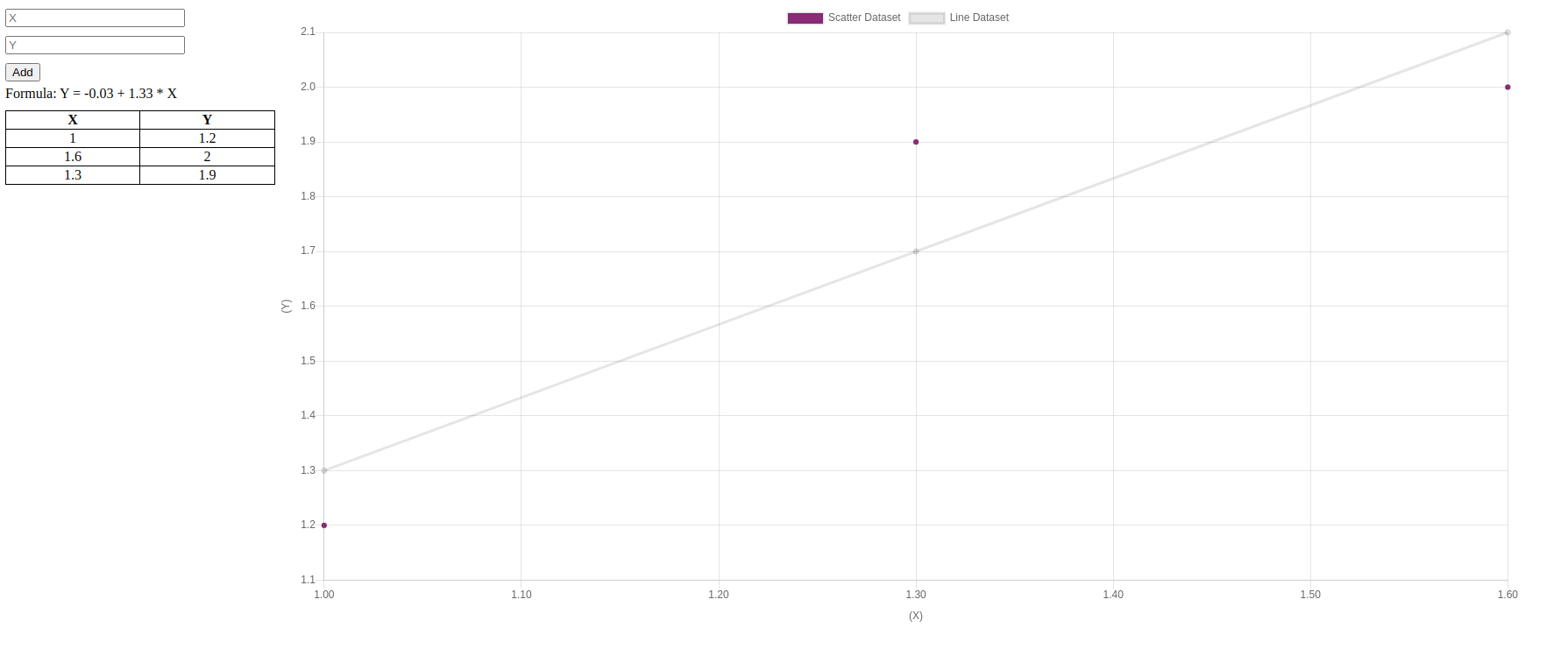
Prova de conceito
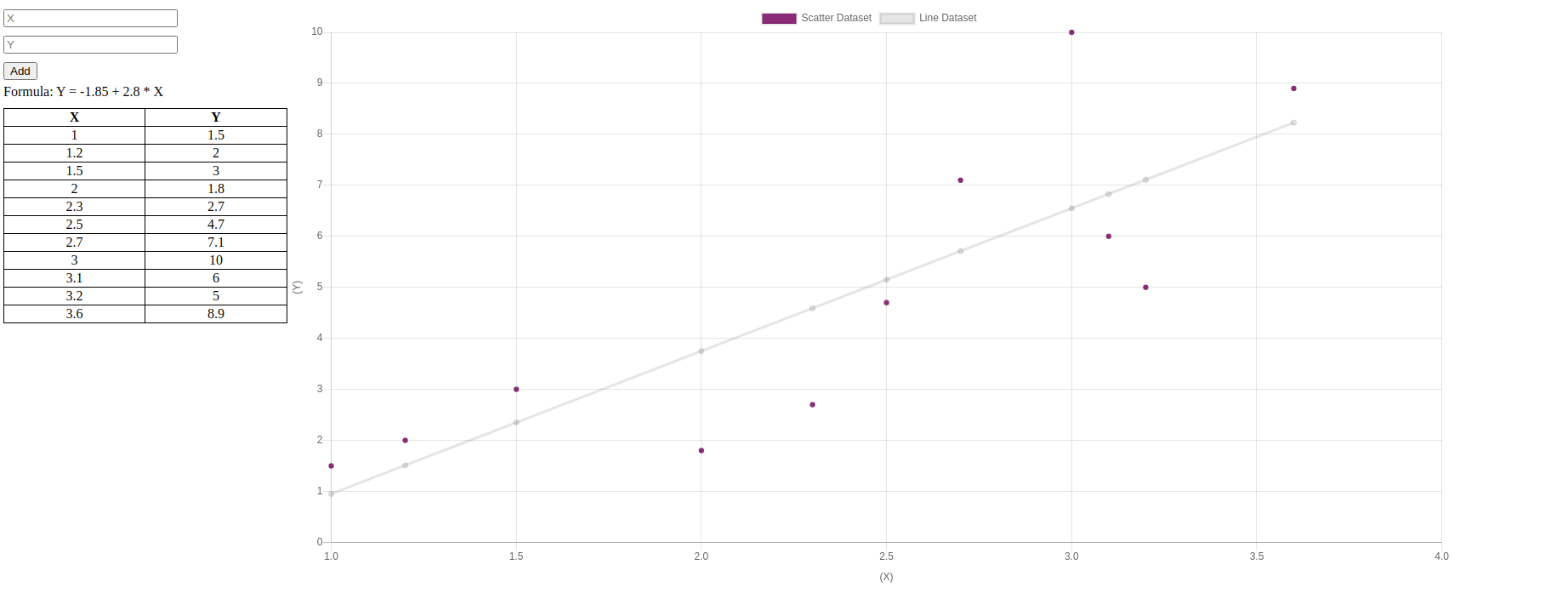
Por uma questão de brevidade, eliminei muitas coisas que podem ser tomadas como um exercício para melhorar muito o projeto. Por exemplo:
- Adicione verificações para valores vazios e semelhantes
- Faça para que possamos remover dados que inserimos incorretamente
- Adicione uma entrada para X ou Y e aplique a fórmula de dados atual para “prever o futuro”, semelhante ao último exemplo da teoria
Independentemente disso, prever o futuro é um conceito divertido, mesmo que, na realidade, o máximo que possamos esperar seja uma aproximação com base em dados anteriores.
É uma fórmula poderosa e se você construir qualquer projeto usando-a, eu adoraria vê-la.
Espero que este artigo tenha sido útil para servir como uma introdução a esse conceito. O código usado no artigo pode ser encontrado em meu GitHub aqui.
Até o próximo, entretanto, vá codificar algo!
